Kombinatorik – die Kunst das Zählens ohne zu Zählen
Verantwortlich | Fachgruppe Mathematik |
Zielgruppen | Schülerinnern und Schüler der Klassen 11-12 |
Gruppengröße | max 12 Schüler |
Themen | Enumerative Kombinatorik |
Dauer | 4 h |
Ort | Hochschule Mittweida |
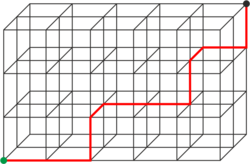
Das nebenstehende Bild zeigt ein Gitter, in dem ein kürzester Weg vom grünen Punkt zum schwarzen Punkt entlang der Gitterlinien angegeben ist. Woher wissen wir, dass es insgesamt 2520 solche Wege gibt? Der Schlüssel für die Lösung ist oft das Finden der richtigen Sprache (die richtigen Beschreibung) für das gegebene Problem. Für die Bestimmung der Anzahl der Gitterwege erweisen sich Wörter über einem Alphabet der Form {a,b,c} als überaus nützlich. So kann der dargestellte Weg in das Wort aabcaabcab „übersetzt“ werden.
Wir schreiben eine Folge von Klammerpaaren, zum Beispiel ((()())()(())). Natürlich sollte niemals, von links nach rechts gelesen, eine schließende Klammer erscheinen, wenn nicht vorher die zugehörige öffnende Klammer auftrat. Wenn wir 10 Klammerpaare verwenden dürfen, so gibt es bereits 16796 Möglichkeiten für eine gültige Klammerfolge. Merkwürdigerweise ist das gleichfalls die Anzahl der Möglichkeiten, ein konvexes Zwölfeck durch Einziehen von Diagonalen in Dreiecke zu zerlegen. Das rechts dargestellte Bild zeigt eine solche Zerlegung.
Viele Fragestellungen, die in Physik, Chemie und Informatik auftreten, führen auf das Zählen bestimmter Konfigurationen. Dabei spielen auch Symmetrie- und Ordnungseigenschaften eine wesentliche Rolle. Wir werden feststellen, dass die moderne Kombinatorik faszinierende Werkzeuge bietet, um auch komplexe Aufgaben dieser Art zu lösen. Neben mathematischen Modellen, wie erzeugende Funktionen, Gruppentheorie und Matrizenalgebra, erweist sich auch Computeralgebra als ein sehr nützliches Instrument für die Lösung von Problemen der enumerativen Kombinatorik.
Wir werden uns Schritt für Schritt an die Lösung recht schwieriger Aufgaben der Kombinatorik wagen, Beschreibungen, Modelle und Gleichungen finden und schließlich, in einigen Fällen mit der Hilfe eines Computers, die Lösung finden.